Εφημερίδα ΒΗΜΑ- Ιωάννα Α. Σουφλέρη
Δώστε μια ευκαιρία στα μαθηματικά να σας γοητεύσουν, τρία βιβλία που παρουσίασε το ΒΗΜΑ. Στην πράξη θα δώσετε μια ευκαιρία στον εαυτό σας να ταξιδέψει σε έναν κόσμο εξαιρετικής αισθητικής.
Αν ανήκετε σε εκείνη την κατηγορία ανθρώπων που ως μαθητές μισούσαν τα μαθηματικά και αν έχετε φροντίσει να τα εξαφανίσετε από τη ζωή σας μετά το λύκειο, τότε ο τίτλος αυτού του άρθρου θα σας φαίνεται οξύμωρο σχήμα. Ξανασκεφτείτε όμως. Ίσως τα μαθηματικά να προκαλούν δέος(ακόμη και αποστροφή) όταν είναι κανείς μαθητής και πρέπει να δώσει εξετάσεις. Αλλά τώρα που έχετε χρόνο, είστε χαλαροί στην παραλία και δεν υπάρχει κανένας να σας επιπλήξει αν δεν βρείτε τη λύση ενός προβλήματος, μπορεί και να τα αγαπήσετε. Δώστε μια ευκαιρία στα μαθηματικά να σας γοητεύσουν, με τα τρία βιβλία που παρουσιάζουμε σήμερα. Στην πράξη θα δώσετε μια ευκαιρία στον εαυτό σας να ταξιδέψει σε έναν κόσμο εξαιρετικής αισθητικής.

Ας αρχίσουμε με κάτι «μαγικό», κάτι με το οποίο θα μπορέσετε να εντυπωσιάσετε τους φίλους σας. Ζητήστε τους να σκεφθούν έναν τριψήφιο αριθμό, οποιονδήποτε τριψήφιο αριθμό, υπό την προϋπόθεση ότι το πρώτο και το τρίτο ψηφίο θα διαφέρουν κατά τουλάχιστον δύο μονάδες. Φυσικά δεν θα σας πουν τον αριθμό που σκέφθηκαν.
Επόμενο βήμα είναι να τους ζητήσετε να αντιστρέψουν αυτόν τον αριθμό και να αφαιρέσουν τον μικρότερο από τον μεγαλύτερο. (Παραδείγματος χάριν, αν σκέφθηκαν το 532, μετά την αντιστροφή το 532 γίνεται 235, το οποίο αφαιρούμενο από το 532 δίνει αποτέλεσμα 297.)
Τρίτο και τελευταίο βήμα είναι να τους ζητήσετε να αντιστρέψουν τον αριθμό που έχει προκύψει από την αφαίρεση και να προσθέσουν τους δύο αριθμούς. (Στην περίπτωση του παραδείγματός μας, αυτό σημαίνει ότι θα προσθέσουν το 297 με το 792.)
Αφού κάνουν όλα αυτά, εσείς θα τους αφήσετε άφωνους μαντεύοντας ότι το αποτέλεσμα αυτής της πρόσθεσης είναι το 1.089 !!
Τον αριθμό 1.089 έχει ως τίτλο το βιβλίο του Βρετανού καθηγητή του Πανεπιστημίου της Οξφόρδης David Αcheson. Όπως σημειώνει ο Αcheson, «το κόλπο του 1.089» ήταν αυτό που τον έπεισε σε ηλικία 10 ετών για το πόσο ενδιαφέρον έχουν τα μαθηματικά. Βλέπετε, αν ακολουθήσετε τους κανόνες, το αποτέλεσμα είναι πάντα 1.089 και δεν εξαρτάται από τον αρχικό αριθμό, αυτόν που τυχαίως θα έχουν επιλέξει οι φίλοι σας.

Τόσο το πόνημα του Αcheson όσο και εκείνο του Λαμπέρτο Γκαρθία δελ Σιδ βρίθουν «κόλπων» τα οποία δεν είναι πάντα δυνατόν να επαναλάβετε στην παραλία, αλλά τα οποία σίγουρα θα σας διασκεδάσουν και θα ακονίσουν το πνεύμα σας. Υπάρχουν μάλιστα και κάποια που μπορεί και να σας προστατεύσουν, ειδικά αν διαθέτετε βλαστάρια που «σκίζουν» στα μαθηματικά, όπως ο Εδουάρδος, που ζητούσε από τον πατέρα του χαρτζιλίκι 5 ευρώ την εβδομάδα ενώ εκείνος ήθελε να του δίνει 3. Σύμφωνα με τον Δελ Σιδ (σελ. 19), ο πιτσιρικάς έκανε στον πατέρα του την εξής πρόταση: να του δίνει για διάστημα ενός μηνός ένα λεπτό του ευρώ την πρώτη ημέρα, δύο την επόμενη, τέσσερα την τρίτη και ούτω καθεξής, ως την τριακοστή. Πρόσθεσε δε ότι από το τέλος του μήνα και μετά δεν θα ήθελε ποτέ πια χαρτζιλίκι. Ο πατέρας του συμφώνησε, για να διαπιστώσει σύντομα το λάθος του: ούτε λίγο ούτε πολύ ως το τέλος του μήνα ο νεαρός θα έπρεπε να εισπράξει 10.737.418,23 ευρώ! Κάντε τις προσθέσεις και θα το διαπιστώσετε...
Από την άλγεβρα και τη γεωμετρία ως την τοπολογία και τη στατιστική, τα βιβλία των Αcheson και Δελ Σιδ διαβάζονται με ή χωρίς σειρά(κάθε κεφάλαιο είναι μια ολοκληρωμένη ενότητα) και αν ακόμη κάπου δυσκολευτείτε με τα μαθηματικά, οι ιστορίες που τα συνοδεύουν(στην περίπτωση του Χαμόγελου του Πυθαγόρα αυτές είναι σε ευδιάκριτους πίνακες) και οι οποίες δεν απαιτούν μαθηματικές γνώσεις θα σας έχουν αποζημιώσει.

Το βιβλίο του Ντενί Γκετζ Το Θεώρημα του παπαγάλου βεβαίως δεν είναι καινούργιο. Η πρώτη ελληνική έκδοσή του χρονολογείται από το 1999. Ωστόσο στην πρόσφατη έκδοσή του το βιβλίο έχει ξαναμεταφραστεί(αριστοτεχνικά, από τον Τεύκρο Μιχαηλίδη) και όσοι δεν το διαβάσατε θα άξιζε τον κόπο να αρχίσετε με αυτό την επαφή σας με τη «μαθηματική λογοτεχνία». Ο Γκετζ δεν παραθέτει γρίφους σαν αυτούς των δύο προηγούμενων βιβλίων. Το βιβλίο του συνδυάζει ένα αστυνομικό μυστήριο με κυριολεκτικά ολόκληρη την ιστορία των μαθηματικών. Οι κεντρικοί ήρωες του, ένας γηραιός βιβλιοπώλης, δύο δίδυμα αδέλφια στην εφηβεία, ο ιδιαίτερα προικισμένος υιοθετημένος μικρός αδελφός τους και η μητέρα τους μοιράζονται την ίδια στέγη στη Μονμάρτρη. Η ζωή τους αναστατώνεται από την άφιξη ενός γράμματος από τα βάθη του Αμαζονίου και ενός παπαγάλου που κρύβει πολλά μυστικά. Με φόντο κυρίως το Παρίσι, αλλά επίσης τη Νότια Ιταλία και την Αμαζονία, ο Γκετζ στήνει μια ιστορία μυστηρίου, για την επίλυση του οποίου οι ήρωες θα χρειαστεί να ανατρέξουν στο σύνολο των μαθηματικών γνωρίζοντάς μας εκείνους που πρωτοστάτησαν στην ανάπτυξη αυτής της επιστήμης. Τόσο διεξοδικός έχει υπάρξει ο Γκετζ ώστε πολλά από τα ιστορικά ανέκδοτα που βρίσκονται στα άλλα δύο βιβλία να υπάρχουν και εδώ. Επίσης, ως «παράπλευρο μπόνους», οι λάτρεις του Παρισιού θα έχουν την ευκαιρία να περπατήσουν στις γειτονιές του.









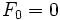 και
και  .
.








